Loading data
By definition, the RNG position right after powering on the PS2 is always 0. However, before you get control of your characters, hundreds of random numbers are consumed during data load. The number of this consumption is not always same, even if you load the same data. I tested using a data at "Cerobi Steppe/Journey's Rest", and the initial RNG position was about 570 +/- 10. Although unconfirmed, this may depend on the model number of your PS2. I used SCPH-70000 for the test.
Actions that do not consume the sequence A
- Opening/closing the menu, change of equipment, moving characters to/from bench, and obtaining a License all consume no random numbers.
- Some Magicks including Blindna, Vox and Dispel consume no random numbers when cast. Also, as far as I know, all actions consume no random numbers if it is interrupted before the charge completes. On the other hand, Battle Ultimania states that a random number is used to calculate a charge time. This means that if Ultimania is correct, a charge time is determined depending on a random number other than one from the sequence A.
- Characters frequently yell when attacking with guns. What they say seem to be randomly chosen from multiple candidates, except that they do not say the same thing twice in a row. On the other hand, we know the use of all of the 8 random numbers consumed from the sequence A when attacking with guns. So it can be guessed that yells are chosen based on another random number sequence than A.
For those interested, I write down what I know about the two other pseudo random number generators found in the game. Both of them are linear congruential generators. Let me formalize the recurrence equations of linear congruential generators as "xn = (xn-1 * a + b) % m". Then one of the generators is specified by the equation (a, b, m) = (6364136223846793005, 1, 264). It outputs ⌊xn / 232⌋ % 231 for each term xn. Its initial value is probably 1. The other is specified by (a, b, m) = (75, 0, 231-1), and it outputs terms without modification. Its initial value is probably 305420679.
Application examples
Identifying RNG position
If you can identify the current RNG position during a play, you will be able to control the game's subsequent random choices to some degree, by adjusting the RNG position adequately. For example, to move the position ahead by 100, shoot yourself 12 times with a gun (when doing this, elemental absorption may keep you alive), then cast Cure 4 times.
An easy way to deduce the current position is to observe damage or healing values. The sequence A can be completely known by calculation, so you can calculate the amount of healing by Curaga for each position in the sequence and put them in a table, for example. Of cource it is not possible to enumerate "all" the RNG positions, but it is usually sufficient to cover the positions below 100,000.
This process is conceptually simple, but doing it by hand is not realistic because it requires a vast amount of calculation. I included a simple JavaScript tool to help this.
Mechanism behind the 5 hit method
The 5 hit method is a reproducible way to obtain rare items from chests, originally found for the IZJS version. The steps are roughly as follows:
- Save near the chest of interest. Reset by hardware.
- Load, and repeat zoning until the chest spawns. If it does not spawn within some repetitions (for example 10), then restart from the beginning.
- Hit yourself repeatedly, with bare hand. Make sure that attacks are never blocked, by either removing a shield or wearing Cameo Belt.
- When a 5 hit combo happens, open the chest, with Diamond Armlet.
- As an additional condition, you may not be attacked by enemies until you open the chest.
This essence of this method is that at the point of opening a chest, the generator A is guranteed to be at the position 1445. The sequence A around 1445 looks like the following.
1444: 2510889783 1445: 1861786791 1446: 1379767799 1447: 80686868
The last two digits of the values at 1445 and 1446 are 91 and 99 respectively, both of which are large. This means that a relatively easy ptest may fail there. Indeed, if you open a chest at the position 1445, both the gil-test and the non-rare test surely fail, because these tests are against at most 90. Consequently you will get a rare item. For your information, in the IZJS version the non-rare test may be against 95, but it still fails because it's compared with 99.
The 5 hit combo itself happens if an unarmed character attacks at the RNG position 1388.
1387: 382760416 1388: 2267807233 Attack here; Knock back chance calculation 1. 1389: 1886692943 Knock back chance calculation 2. 1390: 2131861130 Knock back test 1391: 2952945076 (unknown) 1392: 2341692401 Combo test(against 3) -> Success 1393: 3404601602 Increment-the-number-of-hits test(against 8) -> Success 1394: 2203834536 Increment-the-number-of-hits test(against 8) -> Failure 1395: 961042754 Increment-the-number-of-hits test(against 8) -> Failure 1396: 2005317402 Increment-the-number-of-hits test(against 8) -> Success 1397: 2981387111 Increment-the-number-of-hits test(against 8) -> Failure 1398: 2833431843 Increment-the-number-of-hits test(against 8) -> Failure 1399: 3060953428 Increment-the-number-of-hits test(against 8) -> Failure 1400: 3953158966 Increment-the-number-of-hits test(against 8) -> Failure 1401: 3263761202 Increment-the-number-of-hits test(against 8) -> Success 1402: 161153939 Increment-the-number-of-hits test(against 8) -> Failure 1403: 1977869617 Increment-the-number-of-hits test(against 8) -> Failure; 5 hit Combo 1404: 3808337799 Block-by-shield test(against 0) -> Failure 1405: 3799551709 ...(and so on)...
Since a 5 hit combo consumes 57 random numbers, the position will be 1445 after the combo.
The RNG position moves ahead by 10 each time a character hits herself, if the attack does not combo. Basically this means that in order to reach the position 1388, you must start hitting at a position whose last digit is 8. However, there are two other ways to reach 1388. First, a 4 hit combo happens at 1070, and the position after that combo is 1118, from which you can reach 1388. Similarly, the position 751 causes a 3 hit combo, resulting in the position 790, which leads to 1070. Thanks to these combos, you have a chance to reach 1388 if you start hitting at a position whose last digit is 0, 1 or 8.
As shown above, the RNG position 1388 is relatively easy to reach by repeating hits, causes a infrequent 5 hit combo, and leads to the very good position for opening chests. It is a rare position with this many good properties, and the 5 hit method cleverly uses its speciel characteristic.
Chest spawning laws at "Cerobi Steppe/Crossfield"
In this section I will demonstrate how to investigate individual game processes that involves randomness. As an example, I'll show how I found out the rules that determine whether chests at "Cerobi Steppe/Crossfield" spawn.
According to Scenario Ultimania, p.122, whether a chest spawns or not is determined when you visit the zone. So, as a first step I tried to find out how many random numbers are consumed when entering Crossfield.
First, after a reset, I loaded a data at Journey's Rest, and identified the RNG position using gun damages. Then I entered Crossfield, identified the position again, and calculated the position at the point immedeately after entering the zone. Taking the difference, I saw that 16 random numbers are consumed when I entered Crossfield.
Then I returned to Journey's Rest, reentered Crossfield, and measured the consumption again. This time it consumed only 6 random numbers. This can be understood if we assume that spawning tests of the chests are omitted for this time, because the respawn condition is not met. There are 10 chest positions in Crossfield according to Ultimania, so it makes sense to think that 10 of the first 16 consumptions were for spawning tests.
Now, which of the 16 consumed random numbers were used for spawning tests? According to Ultimania, all the 10 chest positions have spawn rate of 50%. For now let's assume that these spawning tests are actually ptests against 50. The list below shows for each of the 16 consumed numbers, whether ptest against 50 at the position would have succeeded.
n y n n n n n y n y y n n y y n (y means success, n failure)
Next I walked around in Crossfield to check whether individual chests had spawned. There were 4 chests spawned. Using the numbers given by Ultimania, they were 55, 57, 59 and 60.
Let's assume that a contiguous range of the 16 consumption are used for the spawn tests. That is, there should never be a unrelated consumption between two spawn tests. Among the contiguous sublists of the success list above, there are just 2 sublists which have length 10 and contain 4 successes.
n[y n n n n n y n y y]n n y y n and n y n n[n n n y n y y n n y]y n
If the assumptions we have made so far are valid, one of the two sublist represents the range of the RNG table that was used for spawning tests.
It seems that I did't have any more things to say from the data currently available, so I reset the game and collected similar data for another case. I repeated this until I had data for 5 cases.
0: n y n n n n n y n y y n n y y n Appeared: 55, 57, 59, 60 (This is the data discussed above) 1: n y n y n y n y n n n y n y y n y Appeared: 52, 53, 58, 59 2: y n y n y n n n y n y y n y n n y Appeared: 51, 55, 57, 59, 60 3: n y n n y y n n y n y n y n y n n Appeared: 51, 52, 57, 60 4: y n y y n n n n y y n y n n y y Appeared: 51, 53, 56, 60
First, unexpectedly, there were cases where it consumed 17 random numbers (rather than 16) when entering Crossfield. Let's assume there was an extra consumption before or after the chest spawn tests.
I found that under above consumptions, there is only one usage pattern of random numbers. [I used computer to check this, but human calculation could be possible.] It is as follows:
- Consume 1 or 2 random numbers (The usage is not known. It is also not known when it consumes 2.
- Consume a number for each of spawning tests for 10 chest positions. They are tested in order: 55, 53, 51, 52, 54, 58, 57, 56, 60, 59.
- Consume 5 random numbers. According to rémy lachaud, these are used to choose types for traps in the map, one for each.
In total, it consumes 16 or 17 random numbers.
Now we have an idea on how chests in Crossfield spawns. Next we want to test the hypothesis. I restarted the game and tried again. The result was that I was able to successfully predict which chest spawns and which not, for some chest positions. (Yes, I sould have done more thorough test, but I was bored at the work). As a final proof of effectivity, I ensured that I can actually get Ribbon from a chest, by adjusting RNG position to make the chest spawn.
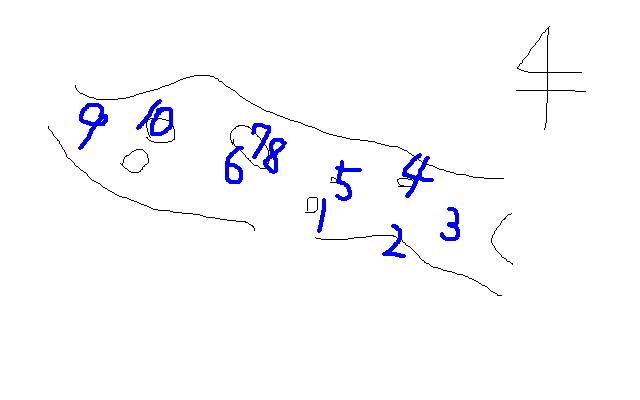
The below is a map of Crossfield, with numbers indicating the order of spawning tests of corresponding chest positions.
Things that is not known
Currently there are more unknown things than known. They include:
- According to p.79, Battle Ultimania, when an attacker is Blind, the gurad rate and parry rate are doubled. However, it turned out that the result of an attack by a Blind character cannot be correctly predicted by simply doubling the threasholds of the guard-by-shield, guard-by-weapon, and parry tests.
- Why is a random number consumption when entering "Cerobi Steppe/Crossfield" not always same? I guess that the weather is relevant, but not confirmed.
- Which item a monster drops?
- Random number consumption in non-battlefields.